1. 分类任务的解释
1.1 二分类
对于一个二分类任务来说,输出层通常使用sigmoid函数,输出一个0-1之间的标量,表示分类为正例的概率。损失函数习惯使用二元交叉熵损失(Binary Cross Entropy Loss):
\[ L_{BCE} = - y \log \hat{y} - (1 - y) \log (1 - \hat{y}) \]
公式解释:
- 当 \(y = 1\) 时:此时样本属于正类别,损失函数变为 \(L(y = 1, \hat{y})=-\log(\hat{y})\)。这意味着当模型预测的正类概率 \(\hat{y}\) 越接近 1 时,损失越小;反之,损失越大。
- 当 \(y = 0\) 时:样本属于负类别,损失函数变为 \(L(y = 0, \hat{y})=-\log(1 - \hat{y})\)。即当模型预测的负类概率 \(1 - \hat{y}\) 越接近 1(也就是正类概率 \(\hat{y}\) 越接近 0)时,损失越小;反之,损失越大。
1.2 多分类
而对于多分类任务来说,输出层通常使用softmax函数,输出一个长度等于类别数量\(C\)的向量\(\hat{y}\),表示每个类别的概率。损失函数习惯使用交叉熵损失(Cross Entropy Loss):
\[ L_{CE} = - \sum_{i=1}^{C} y_{i} \log \hat{y}_{i} \]
公式解释: 一般标签会转为对应的one-hot向量\(y\),只有\(y_i=1\),其他为0(\(i\)为类别标签)。上式可以简化为:
\[ L_{CE} = - \log \hat{y}_i \] 可以看出,交叉熵损失函数只关心正确类别的预测概率,而其他类别的概率则不影响损失值。
如果真实标签不在是一个one-hot向量,而是一个真实概率分布(软标签),比如知识蒸馏任务,可不可以继续用交叉熵损失函数?
2. 使用MSE代替CE来训练分类模型
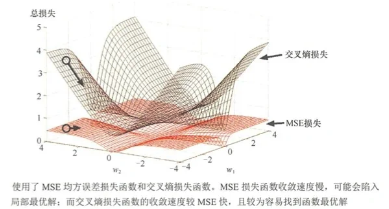
2.1 收敛缓慢
分类问题最后的输出值通常会使用sigmoid或者softmax函数,将输出值转换为概率值(0-1区间),导致MSE损失函数对应的梯度很小,收敛缓慢,并可能陷入局部最优解。
2.2 梯度消失
使用MSE可能出现梯度消失,下面举一个例子:
对于一个二分类问题,最后一层是sigmoid函数,假设真实值为\(y\),预测值为\(\hat{y}\):
$$ \begin{aligned} \hat{y} &= \frac{1}{1 + e^{-\sum_{i=1}^{n} w_i x_i + b}} \\ &= \sigma(\sum_{i=1}^{n} w_i x_i + b) \\ &= \sigma(z) \end{aligned} $$其中sigmoid函数的导数为:
$$ \begin{aligned} \frac{\partial \hat{y}}{\partial w_i} &= \sigma(z)(1 - \sigma(z)) \cdot x_i \\ &= \hat{y}(1 - \hat{y}) \cdot x_i \end{aligned} $$采用MSE损失函数:
$$ \begin{aligned} L_{MSE} &= \frac{1}{2}(\hat{y} - y)^2 \\ \frac{\partial L_{MSE}}{\partial w_i} &= (\hat{y} - y) \cdot \frac{\partial \hat{y}}{\partial w_i} \\ &= (\hat{y} - y) \cdot \hat{y}(1 - \hat{y}) \cdot x_i \end{aligned} $$会产生一下两种无法优化的极端情况(本质上是因为MSE和激活函数不适配?):
- 当\(y=0\)时,预测值\(\hat{y}=1\),梯度为0,无法更新
- 当\(y=1\)时,预测值\(\hat{y}=0\),梯度为0,无法更新
采用CE损失函数:
$$ \begin{aligned} L_{BCE} &= - y \log \hat{y} - (1 - y) \log (1 - \hat{y}) \\ \frac{\partial L_{BCE}}{\partial w_i} &= \frac{\partial L_{BCE}}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial w_i} \\ &= (- \frac{y}{\hat{y}} + \frac{1 - y}{1 - \hat{y}}) \cdot \frac{\partial \hat{y}}{\partial w_i} \\ &= (- \frac{y}{\hat{y}} + \frac{1 - y}{1 - \hat{y}}) \cdot \hat{y}(1 - \hat{y}) \cdot x_i \\ &= (- y(1 - \hat{y}) + (1 - y)\hat{y}) \cdot x_i \\ &= (-y + y\hat{y} + \hat{y} - y\hat{y}) \cdot x_i \\ &= (-y + \hat{y}) \cdot x_i \end{aligned} $$可以看到,使用二元交叉熵损失函数时,不会出现像使用 MSE 损失函数那样在极端情况下梯度为 0 无法更新的问题。即使预测值与真实值偏差很大,梯度依然存在,模型能够继续进行参数更新,从而保证了训练的有效性。
2.3 计算复杂度
通过上面的梯度计算公式可以出,将\(hat{y}\)展开后,MSE的梯度表达式涉及\(w_i\)的三次方,而CE的梯度表达式涉及\(w_i\)的一次方,所以CE的计算复杂度更低。
2.4 不适合分类任务的本质
MSE 损失函数的设计初衷是用于衡量预测值与真实值之间的平均平方误差,它更关注预测值与真实值在数值上的接近程度。而分类任务的核心是将样本正确地划分到不同的类别中,更关注类别之间的区分度。
在分类问题中,我们需要的是一个能够有效放大类别差异的损失函数,使得模型能够快速学习到不同类别之间的边界。MSE 损失函数由于其对所有输出值一视同仁地进行平方误差计算,无法突出类别之间的差异,导致模型在分类任务上表现不佳。而交叉熵损失函数通过对数运算,能够很好地放大预测概率与真实标签之间的差异,更符合分类任务的需求。
交叉熵的本质
信息量、熵、交叉熵、KL散度
一个事件x的信息量\(I(x)\),可以用该事件发生概率\(P(x)\)的对数的负值来衡量,公式为\(I(x)=-\log(P(x))\),概率越低信息量越大。对数的底数不同,信息量的单位也不同。若以 2 为底,单位是比特(bit);以自然常数 e 为底,单位是奈特(nat);以 10 为底,单位是哈特利(Hartley) 。比如,抛一枚均匀硬币,“正面朝上” 这一事件发生概率\(P = 0.5\),其信息量\(I = -\log_20.5 = 1\)比特。
信息熵\(H(X)\)是对随机变量X所有可能事件信息量的期望,公式为\(H(X)=-\sum_{x\in X}P(x)\log(P(x))\)。信息熵代表了随机变量不确定性的平均度量,它描述了整个随机变量的平均信息量。例如,一个离散随机变量X有三个可能取值\(x_1\)、\(x_2\)、\(x_3\) ,概率分别为\(P(x_1)=0.5\) ,\(P(x_2)=0.3\) ,\(P(x_3)=0.2\) ,其信息熵\(H(X)=-(0.5\times\log_20.5 + 0.3\times\log_20.3 + 0.2\times\log_20.2)\approx1.48\)比特 ,表示随机变量X平均所包含的信息量。
交叉熵用于衡量在给定真实概率分布p的情况下,使用近似分布q对信息进行编码所需的平均比特数。假设离散随机变量X的真实概率分布\(p(x)\),近似分布为\(q(x)\),其交叉熵\(H(p,q)\)的计算公式为\(H(p,q)=-\sum_{x}p(x)\log(q(x))\) 。交叉熵越低,说明两个分布越接近。在机器学习的分类任务里,真实分布\(p\)由数据标签给出,模型预测的分布就是\(q\)。最小化交叉熵损失函数,可让模型预测分布更接近真实分布,提高分类准确性。
KL散度(相对熵)用于衡量两个概率分布p和q之间的差异。若离散随机变量X的两个概率分布分别为\(p(x)\)和\(q(x)\) ,KL 散度\(D_{KL}(p||q)\)的计算公式为\(D_{KL}(p||q)=\sum_{x}p(x)\log\frac{p(x)}{q(x)}\) 。KL 散度值为 0 时,意味着两个分布完全相同;值越大,差异越大。它是非对称的,即\(D_{KL}(p||q)\neq D_{KL}(q||p)\) 。在变分自编码器(VAE)等模型中,KL 散度常被用作损失函数的一部分,约束潜在变量的分布,使其接近特定的先验分布,如正态分布。
交叉熵损失函数可以看作是KL散度的一种特殊形式: \[ D_{KL}(p||q) = H(p,q) - H(p) \] 在分类任务任务中,由于真实分布\(p\)是确定的类别,所以\(H(p)=0\),所以往往使用交叉熵损失函数。
那么如果是真实分布是软标签,使用KL散度更加合理,所以在一些蒸馏任务中,往往使用KL散度作为损失函数。



